Like all elementary particles, photons are currently best explained by
quantum mechanics and exhibit
wave–particle duality, exhibiting properties of both
waves and
particles. For example, a single photon may be
refracted by a
lens and exhibit
wave interference with itself, and it can behave as a particle with definite and finite measurable position or
momentum, though not both at the same time. The photon's wave and quantum qualities are two observable aspects of a single phenomenon – they cannot be described by any mechanical model;
[2] a representation of this dual property of light that assumes certain points on the wavefront to be the seat of the energy is not possible. The quanta in a light wave are not spatially localized.
The modern concept of the photon was developed gradually by
Albert Einstein in the early 20th century to explain experimental observations that did not fit the classical
wave model of light. The benefit of the photon model was that it accounted for the frequency dependence of light's energy, and explained the ability of
matter and electromagnetic radiation to be in
thermal equilibrium. The photon model accounted for anomalous observations, including the properties of
black-body radiation, that others (notably
Max Planck) had tried to explain using
semiclassical models. In that model, light was described by
Maxwell's equations, but material objects emitted and absorbed light in
quantized amounts (i.e., they change energy only by certain particular discrete amounts). Although these semiclassical models contributed to the development of quantum mechanics, many further experiments
[3][4] beginning with the phenomenon of
Compton scattering of single photons by electrons, validated Einstein's hypothesis that
light itself is
quantized.
[5][6] In 1926 the optical physicist Frithiof Wolfers and the chemist
Gilbert N. Lewis coined the name "photon" for these particles.
[7] After Arthur H. Compton won the Nobel Prize in 1927 for his scattering studies,
[8] most scientists accepted that light quanta have an independent existence, and the term "photon" was accepted.
In the
Standard Model of
particle physics, photons and other elementary particles are described as a necessary consequence of physical laws having a certain
symmetry at every point in
spacetime. The intrinsic properties of particles, such as
charge,
mass, and
spin, are determined by this
gauge symmetry. The photon concept has led to momentous advances in experimental and theoretical physics, including
lasers,
Bose–Einstein condensation,
quantum field theory, and the
probabilistic interpretation of quantum mechanics. It has been applied to
photochemistry,
high-resolution microscopy, and
measurements of molecular distances. Recently, photons have been studied as elements of
quantum computers, and for applications in
optical imaging and
optical communication such as
quantum cryptography.
Nomenclature[edit]
The word
quanta (singular
quantum, Latin for
how much) was used before 1900 to mean particles or amounts of different
quantities, including
electricity. In 1900, the German physicist
Max Planck was studying black-body radiation: he suggested that the experimental observations would be explained if the energy carried by electromagnetic
waves could only be released in "packets" of energy. In his 1901 article
[9] in
Annalen der Physik he called these packets "energy elements". In 1905,
Albert Einstein published a paper in which he proposed that many light-related phenomena—including black-body radiation and the
photoelectric effect—would be better explained by modelling electromagnetic waves as consisting of spatially localized, discrete wave-packets.
[10] He called such a wave-packet
the light quantum (German:
das Lichtquant).
[Note 1] The name
photon derives from the
Greek word for light,
φῶς (transliterated
phôs).
Arthur Compton used
photon in 1928, referring to
Gilbert N. Lewis.
[11] The same name was used earlier, by the American physicist and psychologist
Leonard T. Troland, who coined the word in 1916, in 1921 by the Irish physicist
John Joly, in 1924 by the French physiologist
René Wurmser (1890–1993) and in 1926 by the French physicist
Frithiof Wolfers (1891–1971).
[7] The name was suggested initially as a unit related to the illumination of the eye and the resulting sensation of light and was used later in a physiological context. Although Wolfers's and Lewis's theories were contradicted by many experiments and never accepted, the new name was adopted very soon by most physicists after Compton used it.
[7][Note 2]
Physical properties[edit]
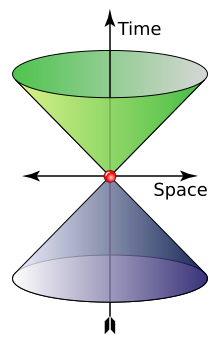
The cone shows possible values of wave 4-vector of a photon. The "time" axis gives the angular frequency (
rad⋅s−1) and the "space" axis represents the angular wavenumber (rad⋅m
−1). Green and indigo represent left and right polarization
In empty space, the photon moves at
c (the
speed of light) and its
energy and
momentum are related by
E = pc, where
p is the
magnitude of the momentum vector
p. This derives from the following relativistic relation, with
m = 0:
[21]
The energy and momentum of a photon depend only on its
frequency (
ν) or inversely, its
wavelength (
λ):


Since p points in the direction of the photon's propagation, the magnitude of the momentum is

The photon also carries a quantity called
spin angular momentum that does not depend on its frequency.
[23] The magnitude of its spin is
√2ħ and the component measured along its direction of motion, its
helicity, must be ±
ħ. These two possible helicities, called right-handed and left-handed, correspond to the two possible
circular polarization states of the photon.
[24]
To illustrate the significance of these formulae, the annihilation of a particle with its antiparticle in free space must result in the creation of at least
two photons for the following reason. In the
center of momentum frame, the colliding antiparticles have no net momentum, whereas a single photon always has momentum (since, as we have seen, it is determined by the photon's frequency or wavelength, which cannot be zero). Hence,
conservation of momentum (or equivalently,
translational invariance) requires that at least two photons are created, with zero net momentum. (However, it is possible if the system interacts with another particle or field for the annihilation to produce one photon, as when a positron annihilates with a bound atomic electron, it is possible for only one photon to be emitted, as the nuclear Coulomb field breaks translational symmetry.)
[25]:64–65 The energy of the two photons, or, equivalently, their frequency, may be determined from
conservation of four-momentum. Seen another way, the photon can be considered as its own antiparticle. The reverse process,
pair production, is the dominant mechanism by which high-energy photons such as
gamma rays lose energy while passing through matter.
[26] That process is the reverse of "annihilation to one photon" allowed in the electric field of an atomic nucleus.
The classical formulae for the energy and momentum of
electromagnetic radiation can be re-expressed in terms of photon events. For example, the
pressure of electromagnetic radiation on an object derives from the transfer of photon momentum per unit time and unit area to that object, since pressure is force per unit area and force is the change in
momentum per unit time.
[27]
Experimental checks on photon mass[edit]
Current commonly accepted physical theories imply or assume the photon to be strictly massless. If the photon is not a strictly massless particle, it would not move at the exact speed of light,
c, in vacuum. Its speed would be lower and depend on its frequency. Relativity would be unaffected by this; the so-called speed of light,
c, would then not be the actual speed at which light moves, but a constant of nature which is the
upper bound on speed that any object could theoretically attain in spacetime.
[29] Thus, it would still be the speed of spacetime ripples (
gravitational waves and
gravitons), but it would not be the speed of photons.
If a photon did have non-zero mass, there would be other effects as well.
Coulomb's law would be modified and the
electromagnetic field would have an extra physical
degree of freedom. These effects yield more sensitive experimental probes of the photon mass than the frequency dependence of the speed of light. If Coulomb's law is not exactly valid, then that would allow the presence of an
electric field to exist within a hollow conductor when it is subjected to an external electric field. This thus allows one to
test Coulomb's law to very high precision.
[30] A null result of such an experiment has set a limit of
m ≲ 10−14 eV/c2.
[31]
Sharper upper limits on the speed of light have been obtained in experiments designed to detect effects caused by the galactic
vector potential. Although the galactic vector potential is very large because the galactic
magnetic field exists on very great length scales, only the magnetic field would be observable if the photon is massless. In the case that the photon has mass, the mass term
1/2m2AμAμ would affect the galactic plasma. The fact that no such effects are seen implies an upper bound on the photon mass of
m < 3×10−27 eV/c2.
[32] The galactic vector potential can also be probed directly by measuring the torque exerted on a magnetized ring.
[33] Such methods were used to obtain the sharper upper limit of
10−18 eV/c2 (the equivalent of
1.07×10−27 atomic mass units) given by the
Particle Data Group.
[34]
These sharp limits from the non-observation of the effects caused by the galactic vector potential have been shown to be model-dependent.
[35] If the photon mass is generated via the
Higgs mechanism then the upper limit of
m ≲ 10−14 eV/c2from the test of Coulomb's law is valid.